21)

△ABC and  △DBC are on the same BC but on opposite sides of it. AD and BC intersect each other at O.If AO = a cm, DO = b cm and the area of △ABC = x cm sq, then what is the area(in cm sq.) of △DBC ?

SSC CGL 2019

A)

\({a\over b}x\)

B)

\({ab\over 2}x\)

C)

\({bx\over a}\)

D)

\({(a+b)\over 2}x\)

22)

In \(\triangle ABC\), the perpendiculars drawn from A, B and C meet the opposite sides at D, E and F, respectively. AD, BE and CF intersect at point P. If \(\angle EPD=116^0\) and the bisectors of \(\angle A\) and \(\angle B\) meet at Q, then the measure of is \(\angle AQB\) is :

SSC CGL 2019

A)

\(96^0\)

B)

\(122^0\)

C)

\(124^0\)

D)

\(64^0\)

23)

The perimeters of two similar triangles ABC and PQR are 78 cm and 46.8 cm, respectively. If PQ = 11.7 cm., then the length of AB is:

SSC CGL 2019

A)

19.5 cm.

B)

23.4 cm.

C)

24 cm.

D)

20 cm.

24)

In \(\triangle PQR\), I is the incentre of the triangle. If \(\angle QIR=107^0\), then what is the measure of \(\angle P\)?

SSC CGL 2019

A)

\(37^0\)

B)

\(43^0\)

C)

\(73^0\)

D)

\(34^0\)

25)

The sides PQ and PR of \(\triangle PQR\) are produced to points S and T, respectively. The bisectors of \(\angle SQR\) and \(\angle TRQ\)meet at U. If \(\angle QUR=79^0\), then the measure of \(\angle P\) is:

SSC CGL 2019

A)

\(41^0\)

B)

\(49^0\)

C)

\(22^0\)

D)

\(23^0\)

26)

In \(\triangle ABC\), AB = AC and D is a point on BC. If BD = 5 cm, AB = 12 cm and AD = 8 cm, then the length of CD is:

SSC CGL 2019

A)

14.8 cm

B)

16.2 cm

C)

16 cm

D)

14 cm

27)

The bisector of \(\angle B\) in \(\triangle ABC\) meets AC at D. If AB = 10 cm, BC = 11 cm and AC = 14 cm, then the length of AD is:

SSC CGL 2019

A)

6 cm

B)

\(22\over3\)cm

C)

7 cm

D)

\(20\over3\) cm

28)

Arrange the angles of the triangle from smallest to largest in the triangle, where the sides are AB = 7 cm, AC = 8 cm, and BC = 9 cm.

SSC CGL 2020

A)

A,B,C

B)

C,B,D

C)

C,B,A

D)

B,A,C

Correct Option: C

C,B,A

---

Measurement of angle is according to the length of opposite line.
So, The order of the angles of the triangle from smallest to largest in the triangle,
C < B < A.

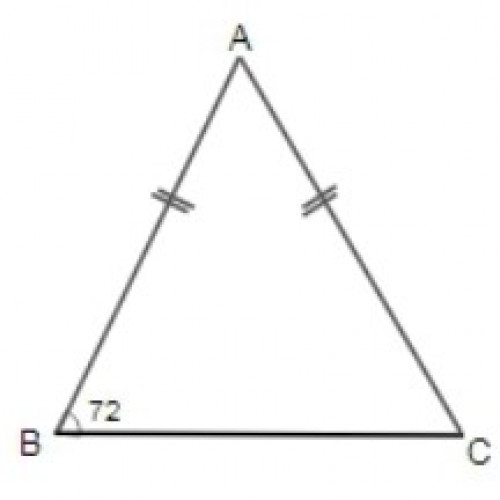
29)

In the triangle, If AB = AC and \(\angle ABC = 72^0\), then \(\angle BAC\)  is:

SSC CGL 2020

A)

\(36^0\)

B)

\(30^0\)

C)

\(18^0\)

D)

\(54^0\)

Correct Option: A

\(36^0\)

---

By triangle properties,
When AB = AC then \(\angle ABC = \angle ACB\) so,
In\(\triangle ABC,\)
\(\Rightarrow  \angle ABC + \angle ACB + \angle BAC = 180^{0}\);
\(\Rightarrow \angle ABC + \angle ABC + \angle BAC = 180^{0}\);
\(\Rightarrow 72^{0} + 72^{0} + \angle BAC = 180^{0}\);
\(\Rightarrow \angle BAC = 180^{0} - 144^{0} = 36^{0}\)

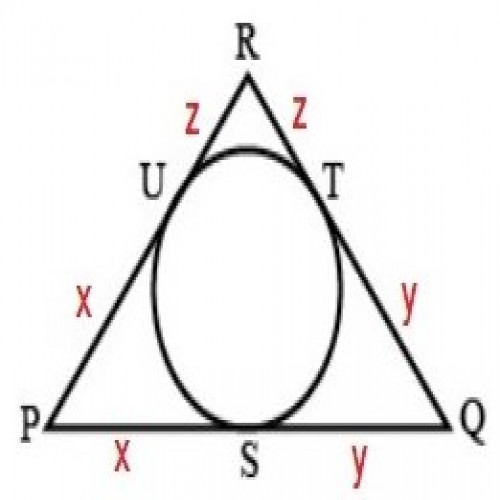
30)

In the given figure, a circle inscribed in triangle PQR touches its sides PQ, QR and RP at points S, T and U,respectively. If PQ = 15 cm, QR= 10 cm, and RP = 12 cm, then find the lengths of PS, QT and RU?

SSC CGL 2020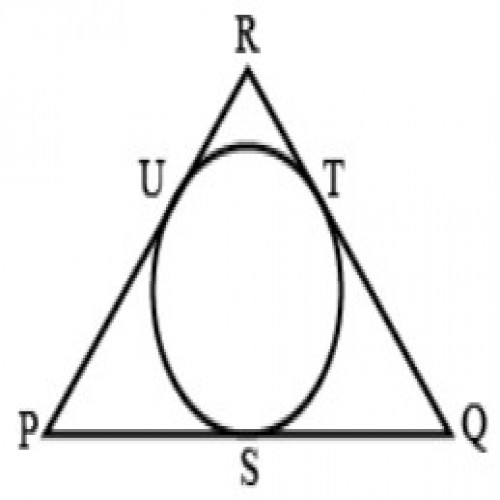

A)

PS = 8.5 cm, QT = 3.5 cm and RU =6.5 cm.

B)

PS = 6.5 cm, QT = 8.5 cm and RU =3.5 cm

C)

PS = 3.5 cm, QT = 6.5 cm and RU = 8.5 cm

D)

PS = 8.5 cm, QT = 6.5 cm and RU = 3.5 cm

Correct Option: D

PS = 8.5 cm, QT = 6.5 cm and RU = 3.5 cm

---

PQ = 15 cm, QR= 10 cm, and RP = 12 cm.  ; 

PQ = x + y = 15------------------(i);  

QR = y + z = 10----------(ii);  

RP = z + x = 12 ------(iii);  

Solving equation, we get : 

 z =  3.5 cm = RU; 

 y  = 6.5 cm = QT; 

 x = 8.5 cm = PS