objective Ques (161 results)
SSC CGL 202031)In \(\triangle ABC,\) D is a point on BC such that AD is the bisector of \(\angle A\), AB = 11.7 cm. AC = 7.8 cm. and BC = 13 cm. What is the length (in cm.) of DC?
5.2
AD is bisector of \(\angle A\).
\({AB\over AC}={BD\over DC}\); Let, BD = x cm. ; DC = (13 - x)cm. ;
\({11.7\over7.8}= {x\over13-x}\); x = 7.8 cm. ;
DC = 13 - 7.8 = 5.2 cm
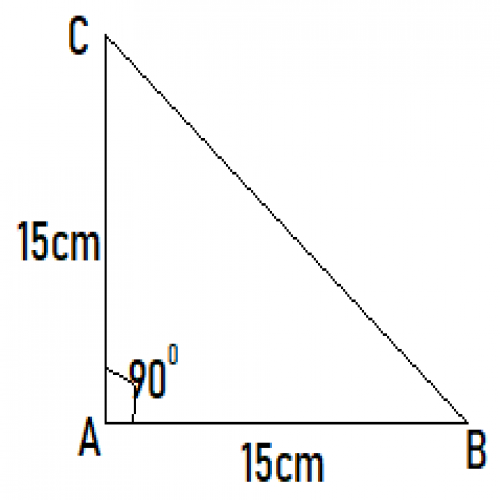
SSC CGL 202032)The length of each equal side of an isosceles triangle is 15 cm and the included angle between those two sides is 90°.Find the area of the triangle.
\({225\over2}cm.^2\)
Area of \(\triangle ABC = {1\over2}\times AB \times AC ={1\over2}\times 15\times 15 ={225\over2} cm^2\)
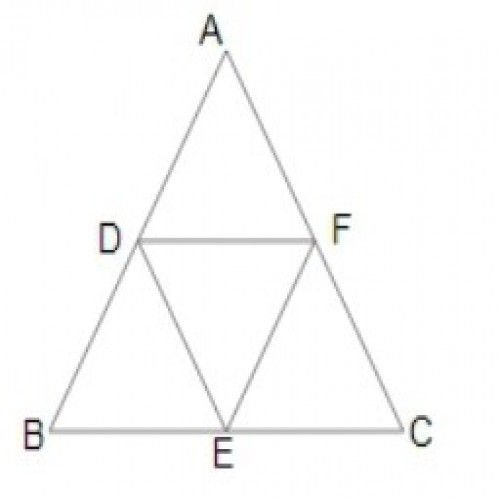
SSC CGL 202033)In \(\triangle ABC\), D, E and F, are the midpoints of sides AB, BC and CA, respectively. If AB = 12 cm, BC = 20 cm and CA = 15 cm, then the value of \({1\over2}(DE+EF+DF)\) is:
11.75 cm
By mid point theorem,
DF = BC/2 = 20/2 = 10 cm;
DE = AC/2 = 15/2 = 7.5 cm;
EF = AB/2 = 12/2 = 6 cm;
\({1\over2}(DF + DE+EF)={1\over2}(10+7.5+6) =11.75\)
34)In the given figure, the measure of \(\angle BAC\) is:
SSC CGL 2020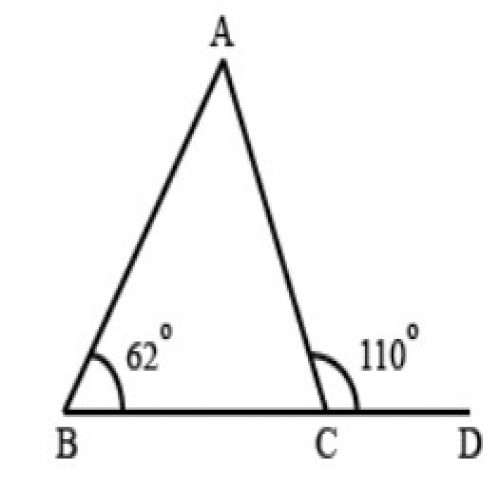
\(48^0\)
In a triangle exterior angle = sum of other two interior angles ; \(\angle ACD = \angle BAC+\angle ABC;\) ⇒ \(\angle BAC= \angle ACD-\angle ABC\) = \(110^0-62^0= 48^0\)
35)In the given figure, \(\triangle ABC\) is an isosceles triangle, in which AB = AC, \(AD \perp BC\), BC = 6 cm. and AD = 4 cm. The length of AB is:
SSC CGL 2020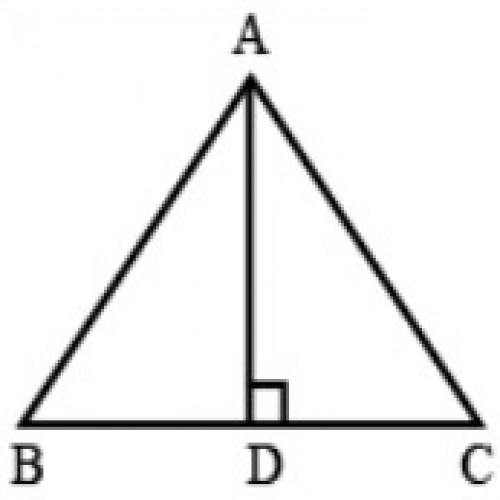
5 cm.
AB = AC; \(\angle ADC=\angle ADB=90^0\); \(\therefore BD = DC\) ; BC = 6 cm. ; BD = \(6\over2\)= 3 cm. ; AD = 4 cm. ; In \(\triangle ABD\), \(AB=\sqrt{AD^2+BD^2}=\sqrt{4^2+3^2}\) = 5 cm.
SSC CGL 202036)In \(\triangle ABC\), if the ratio of angles is in the proportion 3 : 5 : 4, then the difference between the biggest and the smallest angles (in degrees) is:
\(30^0\)
We know that sum of the all angles of the triangle is equal to the \(180^0\) .
Let the angles be 3x, 5x and 4x.
so, 3x + 5x + 4x = 180;
x = 15;
Smallest angle = 3x = 3 x 15 = \(45^0\);
Biggest angle = 5x = 5 x 15 = \( 75^0\);
Difference between the biggest and the smallest angles = 75 - 45 = \(30^0\)
SSC CGL 202037)In a triangle ABC, DE is parallel to BC; AD = a, DB = a + 4, AE = 2a + 3, EC = 7a. What is the value of a if a > 0 ?
3
\(DE\parallel BC\); \(\therefore\angle ADE = \angle ABC\); \(\angle AED = \angle ACB\) ; By AA- similarity theorem, \(\triangle ADE\sim \triangle ABC\); \(\therefore{AD\over AB}={AE\over AC}\) ⇒ \({a\over a+a+4}={2a+3\over 2a+3+7a}\); ⇒ a= 3
SSC CGL 202038)In a triangle, if the measures of two sides are 5 cm and 8 cm, then the third side can be:
4 cm
In a triangle, the sum of two sides is greater than the remaining/ third side. 5 + 2 < 8 ; 5 + 3 = 8 ; 5 + 8 < 14 ; But, 5 + 4 > 8 ; So length of third side = 4 cm
39)In the given figure, if AB = 10 cm, \(\angle ABD = 90^0\) and AD = 17 cm, then the measure of CD is:
SSC CGL 2020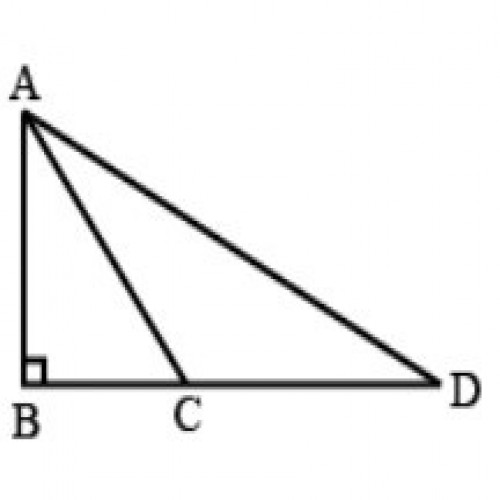
9 cm
In \(\triangle ABC\), AB = 8 cm ; AC = 10 cm; \(\therefore BC = \sqrt{AC^2-AB^2}=\sqrt{10^2-8^2}=6\space cm\); In \(\triangle ABD\), AD = 17 cm ; \(\therefore BD =\sqrt{AD^2-AB^2}=\sqrt{17^2-8^2}= 15 \space cm\) ; So CD = 15 - 6 = 9 cm
SSC CGL 202040)If the area of an equilateral triangle is \(36\sqrt3\space cm^2\), then the perimeter of the triangle is:
36 cm
Area of an equilateral triangle = \(36\sqrt3\space cm^2\); ⇒ \({\sqrt3\over4}\times Side^2= 36\sqrt3\); ⇒ Side = 12 cm ; Therefore, Perimeter of triangle = \(3\times Side\) = 36 cm