objective Ques (105 results)
SSC CGL 20201)What is the area of a sector of a circle of radius 14 cm and central angle 45 degree? take \(\pi = {22 \over 7} \)
77 sqcm
Area of Sector = \(x = \pi r^2 .{\theta \over 360 } = 77 cm^2\)
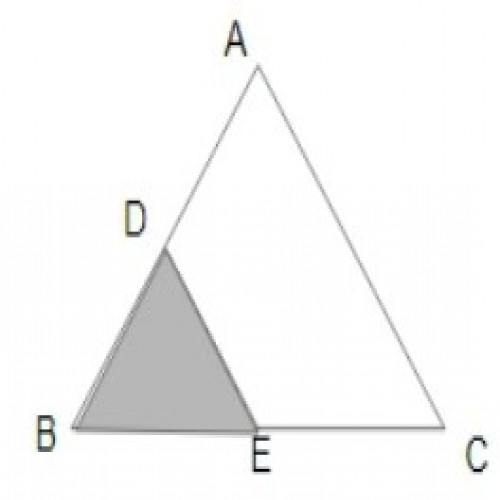
SSC CGL 20192)In \(\triangle ABC\), D and E are the points on sides AB and BC respectively such that DE||AC . If AD : DB = 5 : 3, then what is the ratio of the area of \(\triangle BDE\) to that of the trapezium ACED?
9 : 55
\(\triangle ABC ~ \triangle DEB;\)
(\because DE is parallel to AC);
\(\angle B\) is a common angle.
So, ratio area of the \( \triangle BDE : \triangle ABC \);
\((3)^2 : (3 + 5)^2\) = 9 : 64;
Area of trapezium ACED = area of the \(\triangle ABC - \triangle BDE \)= 64 - 9 = 55;
Ratio of the area of\( \triangle BDE\) to that of the trapezium ACED = 9 : 55
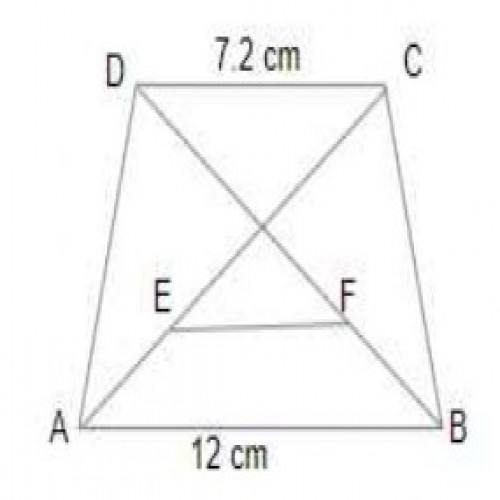
SSC CGL 20193)In a trapezium ABCD, \(DC \parallel AB \), AB = 12 cm and DC = 7.2 cm. What is the length of the line segment joining the midpoints of its diagonals?
2.4 cm
By the property, EF = \(\frac{AB - CD}{2} = \frac{12 - 7.2}{2} = \frac{4.8}{2} \)= 2.4 cm
SSC CGL 20194)A field roller, in the shape of a cylinder, has a diameter of 1 m and length of \(1\frac{1}{4}\) m. If the speed at which the roller rolls is 14 revolutions per minute, then the maximum area (in square m ) that it can roll in 1 hour is: (Take \(\pi={22\over7}\) )
3300
Area covered in single revolution = \(2 \pi rh\) ;
Area covered in 1 hour = \({2\times {22\over 7} \times {1\over 2} \times {5\over 4} \times 14 \times 60} = 3300 cm^2\)
SSC CGL 20205)A wheel covers a distance of 1,100 cm in one round. The radius of the wheel is :
175 cm
A wheel covers a distance of 1,100 cm in one round so,
Perimeter of wheel = 1100 cm;
\(2\pi r\) = 1100;
r = \(550\times\frac{7}{22}\) = 175 cm;
Diameter = 2r = 2 175 = 350 cm
SSC CGL 20206)The perimeter of a square plot is the same as that of a rectangular plot with sides 35 m and 15 m. The side of the square plot is:
25 metre
The perimeter of a rectangular plot = 2(length + breadth) = 2(35 + 15) = 100 m;
The perimeter of a square plot = perimeter of a rectangular plot;
The perimeter of a square plot = 100 m;
100 = 4 side;
side = 100/4 = 25 m
SSC CGL 20207)What is the area of a triangle whose sides are 3 cm, 5 cm and 4 cm?
\(6\) \(cm^2\)
By triplet 3-4-5, the triangle will be right angle triangle so,
5 will be hypotenuse.
Area of triangle = \({1\over2}\times base\times height\) = \({1\over2}\times3\times4 = 6 \) \(cm^2\)
SSC CGL 20208)Find the area and circumference of a circle if the radius is 14 cm.(Take \(\pi= {22\over7}\))
Area = \(616 \)\(cm^2\); circumference = 88 cm
Radius of circle = 14 cm. ;
Area of circle = \(\pi r^2={22\over7}\times{(14)^2}= 616 cm^2\);;
Circumference of circle = \(2\pi r = 2\times{22\over7}\times 14 = 88 cm\)
SSC CGL 20209)If the perimeter of a certain rectangle is 50 units and its area is 150 sq. units, then how many units is the length of its shorter side?
10
Let, the length of rectangle= x units; Its width = y units; According to the question, 2(x+y) = 50;
x + y = 25 ---(1) ; and, xy = 150___(2); \((x-y)^2=(x+y)^2-4xy\) \(=(25)^2-4\times150=25\); ⇒ \(x-y=\sqrt{25} =5\)____(3);
By equation (1) - (3) we have; x + y - x + y = 25 - 5 = 20; So y = 10 units
SSC CGL 202010)The perimeter of an isosceles triangle is 50 cm.If the base is 18 cm, then find the length of the equal sides.
16 cm
Let Each equal side of isosceles triangle = x cm.
According to the question, x + x + 18 = 50; ⇒ x = 16 cm.
Full Syllabus in 1 Video [Contains Everything basic to advance]