1)

In the figure, PA is a tangent from an external point P to the circle with centre O. If \(\angle POB = 110 ^{\circ}\), then measure of \(\angle APO\) is:

SSC CGL 2020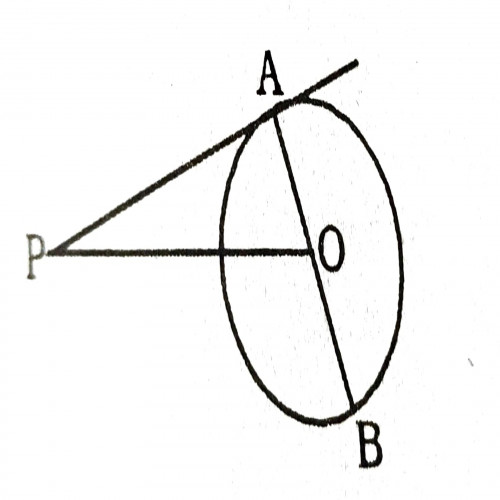

A)

\(30 ^{\circ}\)

B)

\(25^{\circ}\)

C)

\(20 ^{\circ}\)

D)

\(40 ^{\circ}\)

2)

If angle of sector is 60°, radius is 3.5 cm then length of the arc is

Class 10 Maths

A)

3.66 cm

B)

3.56 cm

C)

1.66 cm

D)

3 cm

3)

Chord AB of a circle is produced to a point P, and is a point on the circle such that PC is a tangent to the circle. If PC = 18 cm, and BP = 15 cm, then AB is equal to:

SSC CGL 2019

A)

5.8 cm

B)

6.2 cm

C)

6.6 cm

D)

8.5 cm

Correct Option: C

6.6 cm

---

By the property,
\(PC^2 = PA \times PB;\)
\((18)^2 = PA \times 15;\)
PA = 324/15 = 21.6 cm;
AB = PA - PB = 21.6 - 15 = 6.6 cm

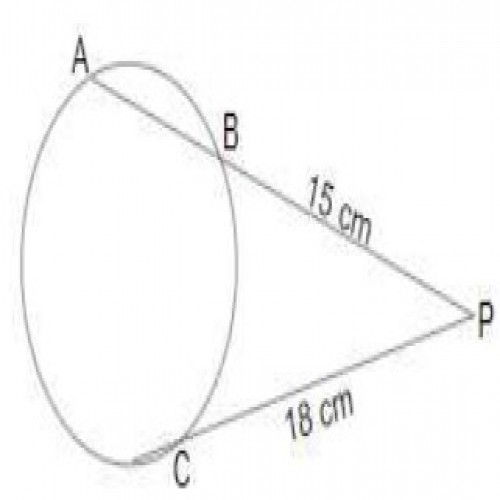
4)

Two parallel chords on the same side of the centre of a circle are 12 cm and 20 cm long and the radius of the circle is \(5\sqrt{13}cm\). What is the distance (in cm) between the chords?

SSC CGL 2019

A)

2

B)

3

C)

2.5

D)

1.5

5)

A circle touches the side BC of \(\triangle ABC\) at D and AB and AC are produced to E and F, respectively. If AB = 10 cm, AC = 8.6 cm and BC =6.4 cm, then BE =?

SSC CGL 2019

A)

3.2 cm

B)

3.5 cm

C)

2.2 cm

D)

2.5 cm

6)

In circle with centre O, AC and BD are two chords. AC and BD meet at E when produced. If AB is the diameter and \(\angle AEB=68^0\), then the measure of \(\angle DOC\) is :

SSC CGL 2019

A)

\(32^0\)

B)

\(30^0\)

C)

\(22^0\)

D)

\(44^0\)

7)

In a circle, AB and DC are two chords. When AB and DC are produced, they meet at P. If PC = 5.6 cm, PB = 6.3 cm and AB = 7.7 cm, then the length of CD is:

SSC CGL 2019

A)

8.35 cm.

B)

9 cm.

C)

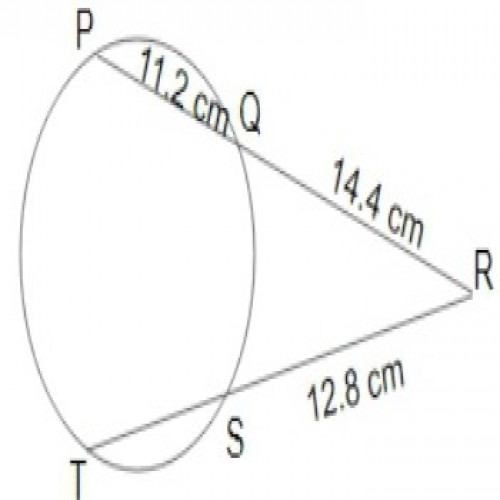
10.15 cm.

D)

9.25 cm.

8)

In a circle, chords PQ and TS are produced to meet at R. If RQ = 14.4 cm, PQ = 11.2 cm, and SR = 12.8 cm, then the length of chord TS is:

SSC CGL 2020

A)

18 cm

B)

14.2 cm

C)

12.4 cm

D)

16 cm

Correct Option: D

16 cm

---

RQ X PR = RS X TR;  14.4 X (14.4+11.2) = 12.8 X TR;  TR = \({14.4\times25.6\over12.8}=28.8 cm\) ;  TS = TR - SR = (28.8 - 12.8) cm = 16 cm

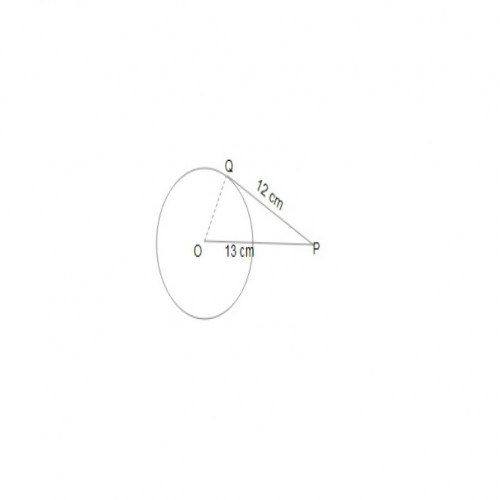
9)

From an external point P, a tangent PQ is drawn to a circle, with the centre O, touching the circle at Q. If the distance of P from the centre is 13 cm and length of the tangent PQ is 12 cm, then the radius of the circle is:

SSC CGL 2020

A)

3 cm

B)

12.5 cm

C)

5 cm

D)

10 cm

Correct Option: C

5 cm

---

\triangle OPQ is a right angle triangle because \(\angle Q = 90^0\),
By Pythagoras,
\((OQ)^2 + (PQ)^2 = (OP)^2\);
\((OQ)^2 = (13)^2 - (12)^2\);
\((OQ)^2\) = 169 - 144;
\((OQ)^2\) = 25;
OQ = 5 cm.

10)

In a circle, AB is a the diameter and CD is a chord. AB and CD produced meet at a point P, outside the circle. If PD = 15.3 cm, CD = 11.9 cm and AP = 30.6 cm,then the radius of the circle is is:

SSC CGL 2020

A)

7.5 cm

B)

8.5 cm

C)

9 cm

D)

8 cm

Correct Option: B

8.5 cm

---

From the property,
\(PA \times PB = PC \times PD\);
\(30.6 \times PB = (PD + CD) \times 15.3\);
\(30.6 \times PB = (15.3 + 11.9) \times 15.3\);
\(30.6 \times PB = 27.2 \times 15.3\);
PB = 416.16/30.6 = 13.6 cm;
Diameter (AB) = PA - PB = 30.6 - 13.6 = 17 cm;
Radius = AB/2 = 17/2 = 8.5 cm