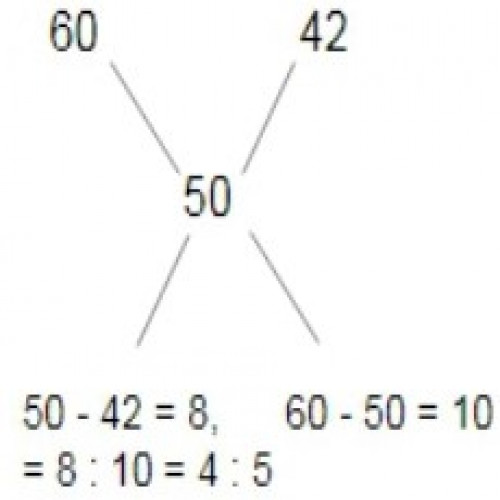
1)

In what ratio, sugar costing Rs.60 per kg be mixed with sugar costing Rs.42 per kg such that by selling the mixture at Rs.56 per kg there is a gain of 12%?

SSC CGL 2019

A)

5 : 6

B)

8 : 9

C)

4 : 5

D)

5 : 7

Correct Option: C

4 : 5

---

Selling price of mixture = 56;
profit = 12%;
Cost price of the mixture =\( 56 \times \frac{100}{112}\) = Rs. 50;
By allegation method,

2)

The ratios of copper to zinc in alloys A and B are 3 : 4 and 5 : 9, respectively. A and B are taken in the ratio 2 : 3 and melted to form a new alloy C. What is the ratio of copper to zinc in C?

SSC CGL 2019

A)

8 : 13

B)

3 : 5

C)

9 : 11

D)

27 : 43

3)

A vessel contains a 32 litre solution of acid and water in which the ratio of acid and water is 5 : 3, If 12 litres of the solution are taken out and \(7\frac{1}{2}\)itres of water are added to it, then what is the ratio of acid and water in the resulting solution?

SSC CGL 2019

A)

4 : 7

B)

5 : 6

C)

4 : 9

D)

8 : 11

4)

How many kg of salt costing ₹28 per kg must be mixed with 6.6 kg of salt costing ₹16 per kg, so that selling the mixture at ₹29.90, there is a gain of 15%?

SSC CGL 2019

A)

33

B)

31

C)

35

D)

32

5)

40 litres of 60% concentration of acid solution is added to 35 litres of 80% concentration of acid solution. What is the concentration of acid in the new solution?

SSC CGL 2019

A)

66%

B)

\(66\frac{2}{3}\)%

C)

\(69\frac{1}{3}\)%

D)

69%

6)

Alloy A contains copper and zinc in the ratio of 4 : 3 and alloy B contains copper and zinc in the ratio of 5: 2. A and B are taken in the ratio of 5 : 6 and melted to form a new alloy. The percentage of zinc in the new alloy is closest to:

SSC CGL 2019

A)

54

B)

34.2

C)

36.8

D)

35

7)

25 litres of a mixture contains 30%of spirit and rest water. If 5 litres of water be mixed in it, the percentage of spirit in the new mixture is :

SSC CGL 2020

A)

\(12{1\over2}\)%

B)

\(33{1\over3}\)%

C)

25%

D)

45%

8)

A solution contains acid and water in the ratio of 4 : 5. If 20% of the solution is replaced by water, then what will be the ratio of acid and water in the new solution?

SSC CHSL 2021

A)

8 : 15

B)

5 : 17

C)

10 : 7

D)

16 : 29

9)

A shopkeeper mixes three varieties of tea costing Rs 60 per kg, Rs80 per kg, and Rs120 per kg in the ratio 5 : 8 : 7. At what price (in Rs) per kg should he sell the tea mixture to earn a 25% profit?

SSC Selection Post Matric 2022

A)

86.67

B)

100.33

C)

111.25

D)

104.50

10)

A person bought 20 kg of oranges at Rs. 64/kg, 25 kg of oranges at Rs. 56/kg and Rs. 35 kg of oranges at Rs. 50/kg. He mixed the three varieties. If he sells the whole lot at Rs. 63.75/kg, then his profit percentage is: (correct to the nearest integer)

SSC Selection Post Matric 2022

A)

18%

B)

 15%

C)

12%

D)

13%