objective Ques (161 results)
1)दी गई आकृति में, \(\triangle ABC\) में, यदि \(\theta = 80^o\) है, तो अन्य दो में से प्रत्येक कोण की माप क्या होगी ?
SSC CGL 2020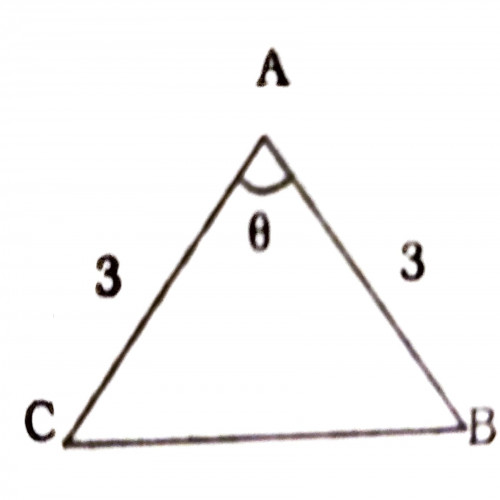
\(50^0\)
since the two sides are equal in length, and equal side corresponds equal angle, therefore \(2x + \theta = 180\), x = 50
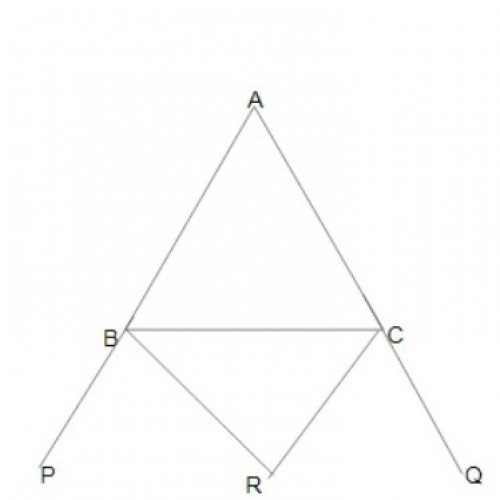
SSC CGL 20192)\( {\Delta ABC}\) की भुजाएँ AB और AC क्रमशः P और Q तक बढ़ाई जाती हैं । \({\angle CBP}\) और \({\angle BCQ}\) के समद्विभाजक R पर मिलते हैं । यदि \({\angle A}\) का माप 44º है, तो \({1\over2 }\)\({\angle BRC}\) का माप क्या है ?
34º
\(\angle BRC = 90 ^o - \angle A/2; = 90 ^o - 44^o/2 = 90 ^o - 22^o = 68^o; \frac{1}{2} \angle BOC = \frac{68^o}{2}; \frac{1}{2} \angle BOC = 34^o;\)
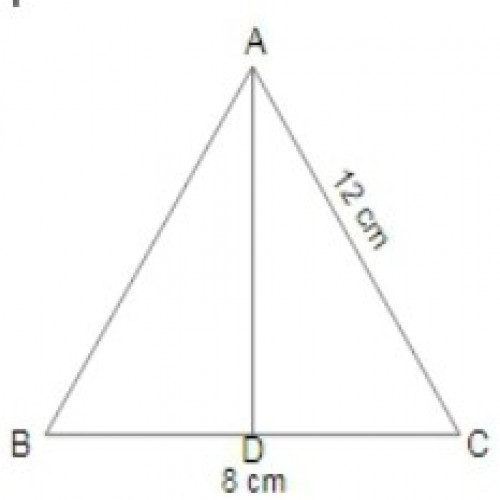
SSC CGL 20193)\( {\Delta ABC}\) में, बिंदु D भुजा BC पर इस प्रकार है कि \({\angle ADC}={\angle BAC}\) होता है । यदि CA = 12 cm, CB = 8 cm, तो CD निम्नलिखित में किसके बराबर है ?
18 cm.
\(\angle ADC = \angle BAC; \angle ACB = \angle ACD; So, \triangle ABC ~ \triangle DCA,; So, \frac{BC}{AC} = \frac{AC}{CD}; \frac{8}{12} = \frac{12}{CD};\)
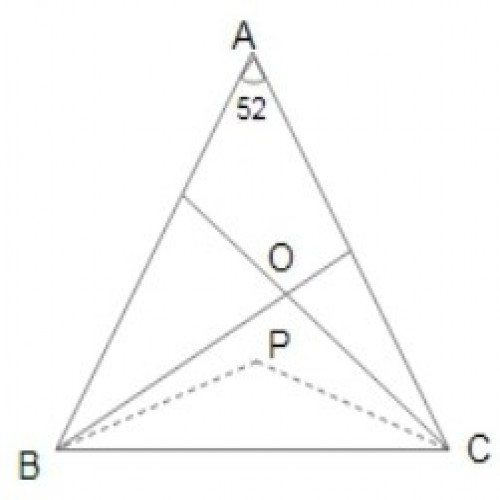
SSC CGL 20194)\({\Delta ABC}\) में, \(\angle A =52^0\) और O त्रिभुज का लम्बकेन्द्र है (BO और CO, तब क्रमशः E और F पर AC एवं AB से मिलते हैं जब उन्हें प्रोड्यूस किया जाता है)। यदि \({\angle OBC} \) और \({\angle OCB}\) के समद्विभाजक P पर मिलते हैं, तो \({\angle BPC}\) का माप है |
154º
By the orthogonal property,
\(\angle BOC = 180 - \angle A\);
\(\angle OBC + \angle OCB = \angle A;\)
\(\angle BPC = 180 - \angle A/2;\)
\(\angle BPC = 180 - \angle 52/2 = 180 - 26 = 154^0\)
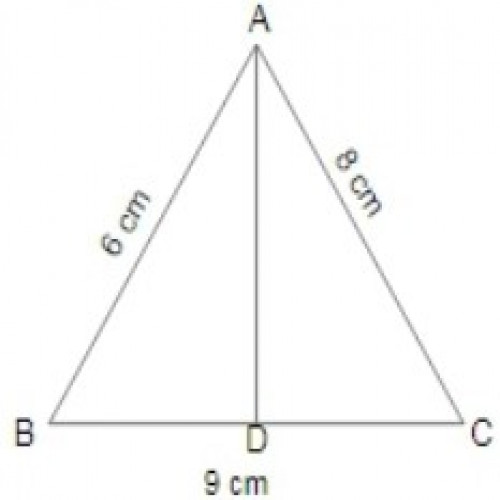
SSC CGL 20195)\(\Delta ABC\) में, AB = 6 cm, AC = 8 cm, और BC = 9 cm है । माध्यिका AD की लंबाई है |
\({\sqrt{119}\over 2}\) cm
In ΔABC, AD is median . D. will be the mid point of BC.
BD = CD = BC/2= 9/2 = 4.5 cm;
\(AB^2 + AC^2 = 2(AD^2 + BD^2);\)
\(6^2 + 8^2 = 2(AD^2 + (4.5)^2);\)
\(100/2 = AD^2 + 20.25\);
\(AD^2 = 29.75 = 119/4;\)
\(AD = \frac{\sqrt{119}}{2}\)
SSC CGL 20196)\( \triangle ABC\) में, AB=7cm, BC=10cm, और AC = 8cm है। यदि AD, \(\angle BAC\) का कोण समद्विभाजक है, जहाँ D, BC पर एक बिंदु है, तो BD निम्नलिखित में से किसके बराबर है ?
\({14 \over3}cm\)
Let the BD = x,
DC = 10 - x
By angle bisector theorem,
\(\frac{BD}{CD}\) =\( \frac{AB}{AC} \); \(\frac{x}{10 - x}\) = \(\frac{7}{8}\)
8x = 70 - 7x
15x = 70
x = 14/3 cm
BD = \(\frac{14}{3}\)
SSC CGL 20197)एक त्रिभुज की भुजाएँ 11 सेमी, 60 सेमी और 61 सेमी हैं । त्रिभुज का परिवृत्त बनाने वाले वृत्त की त्रिज्या क्या है ?
30.5 cm
Radius of the circle circumference = hypotenuse/2 = 61/2 = 30.5 cm
SSC CGL 20198)\( \triangle ABC\) में, \( \angle A = 58^\circ\) है । यदि I त्रिभुज का अंतःकेंद्र है तो \(\angle BIC\) का माप है |
\(119^0\)
\(\angle BIC = 90^0 + \angle A/2\);
\(\angle BIC = 90^0+ 58/2 = 90^0 + 29^0 = 119^0\)
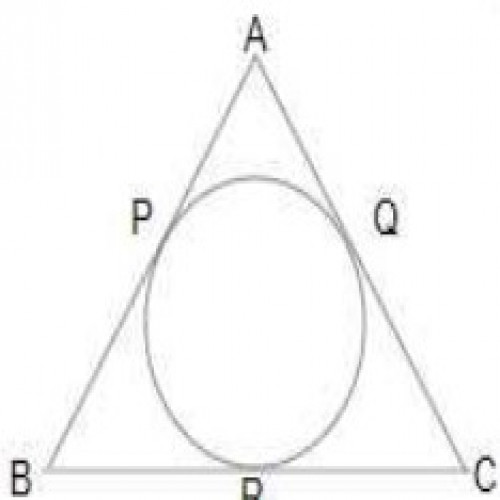
SSC CGL 20199)\( \triangle ABC\) के भीतर एक वृत्त बनाया गया है, जो क्रमशः AB, BC और AC को बिंदु P, Q और R बिंदु पर स्पर्श करता है । यदि AB - BC = 4 cm, AB - AC = 2 cm और \( \triangle ABC\) का परिमाप = 32 cm है, तो PB + AR निम्नलिखित में किसके बराबर है ?
\(38\over3\) cm
Perimeter = 32 cm;
AB + BC + AC = 32 cm ---(1);
AB - BC = 4 cm ---(2);
AB - AC = 2 cm ---(3);
On eq(1) + (2) + (3),
3AB = 38;
AB = PB + AR = 38/3
SSC CGL 201910)एक त्रिभुज की भुजाएँ 12 सेमी, 35 सेमी और 37 सेमी हैं । त्रिभुज की परिधि(circumradius) क्या है ?
18.5 सेमी