objective Ques (161 results)
SSC CGL 202031)\(\triangle ABC\) में, D, BC पर एक ऐसा बिंदु है कि AD, \(\angle A\) का समद्विभाजक है, AB = 11.7 सेमी. AC = 7.8 सेमी और BC = 13 सेमी । DC की लंबाई (सेमी में) क्या है ?
5.2
AD is bisector of \(\angle A\).
\({AB\over AC}={BD\over DC}\); Let, BD = x cm. ; DC = (13 - x)cm. ;
\({11.7\over7.8}= {x\over13-x}\); x = 7.8 cm. ;
DC = 13 - 7.8 = 5.2 cm
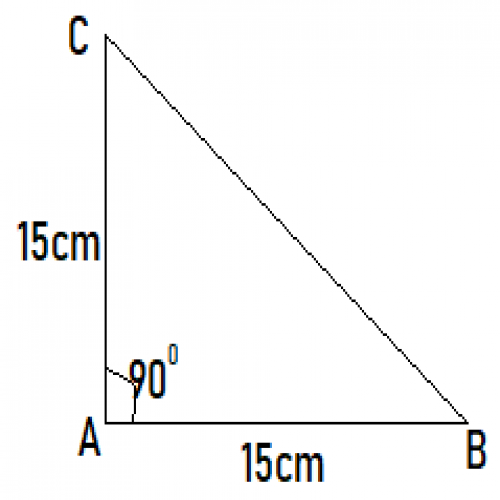
SSC CGL 202032)एक समद्विबाहु त्रिभुज की प्रत्येक समान भुजा की लंबाई 15 सेमी है और उन दोनों भुजाओं के बीच का कोण 90° है । त्रिभुज का क्षेत्रफल ज्ञात कीजिए ।
\({225\over2}cm.^2\)
Area of \(\triangle ABC = {1\over2}\times AB \times AC ={1\over2}\times 15\times 15 ={225\over2} cm^2\)
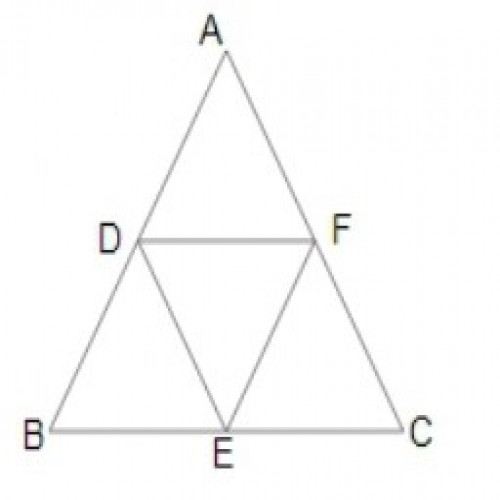
SSC CGL 202033)\(\triangle ABC\) में, D, E और F क्रमशः भुजाओं AB, BC और CA के मध्यबिंदु हैं । यदि AB = 12 सेमी, BC = 20 सेमी और CA = 15 सेमी, तो \({1\over2}(DE+EF+DF)\) का मान है |
11.75 cm
By mid point theorem,
DF = BC/2 = 20/2 = 10 cm;
DE = AC/2 = 15/2 = 7.5 cm;
EF = AB/2 = 12/2 = 6 cm;
\({1\over2}(DF + DE+EF)={1\over2}(10+7.5+6) =11.75\)
34)दी गई आकृति में, \(\angle BAC\) का माप है :
SSC CGL 2020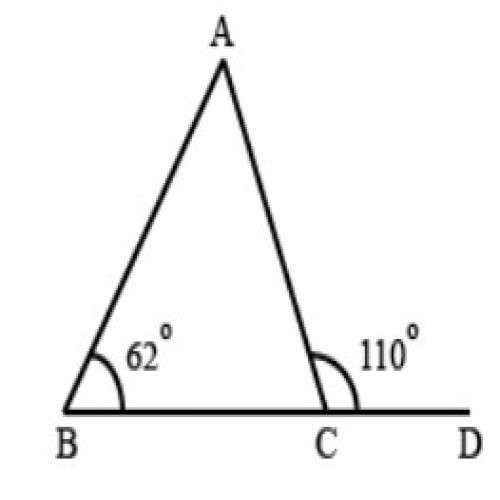
\(48^0\)
In a triangle exterior angle = sum of other two interior angles ; \(\angle ACD = \angle BAC+\angle ABC;\) ⇒ \(\angle BAC= \angle ACD-\angle ABC\) = \(110^0-62^0= 48^0\)
35)दी गई आकृति में, \(\triangle ABC\) एक समद्विबाहु त्रिभुज है, जिसमें AB = AC, AD⊥BC, BC = 6 सेमी है और AD = 4 सेमी. AB की लंबाई है |
SSC CGL 2020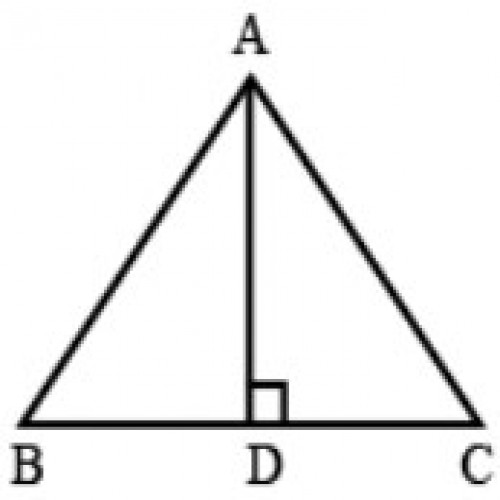
5 सेमी.
AB = AC; \(\angle ADC=\angle ADB=90^0\); \(\therefore BD = DC\) ; BC = 6 cm. ; BD = \(6\over2\)= 3 cm. ; AD = 4 cm. ; In \(\triangle ABD\), \(AB=\sqrt{AD^2+BD^2}=\sqrt{4^2+3^2}\) = 5 cm.
SSC CGL 202036)\(\triangle ABC\) में, यदि कोणों का अनुपात 3 : 5 : 4 है, तो सबसे बड़े और सबसे छोटे कोणों के बीच का अंतर क्या होगा (डिग्री में) ?
\(30^0\)
We know that sum of the all angles of the triangle is equal to the \(180^0\) .
Let the angles be 3x, 5x and 4x.
so, 3x + 5x + 4x = 180;
x = 15;
Smallest angle = 3x = 3 x 15 = \(45^0\);
Biggest angle = 5x = 5 x 15 = \( 75^0\);
Difference between the biggest and the smallest angles = 75 - 45 = \(30^0\)
SSC CGL 202037)त्रिभुज ABC में, DE BC के समांतर है, AD = a, DB = a + 4, AE = 2a + 3, EC = 7a है । यदि a>0 है, तो 'a' का मान ज्ञात कीजिए ।
3
\(DE\parallel BC\); \(\therefore\angle ADE = \angle ABC\); \(\angle AED = \angle ACB\) ; By AA- similarity theorem, \(\triangle ADE\sim \triangle ABC\); \(\therefore{AD\over AB}={AE\over AC}\) ⇒ \({a\over a+a+4}={2a+3\over 2a+3+7a}\); ⇒ a= 3
SSC CGL 202038)एक त्रिभुज में, यदि दो भुजाओं की लंबाई 5 cm और 8 cm है, तो तीसरी भुजा की लंबाई कितनी हो सकती है ?
4 cm
In a triangle, the sum of two sides is greater than the remaining/ third side. 5 + 2 < 8 ; 5 + 3 = 8 ; 5 + 8 < 14 ; But, 5 + 4 > 8 ; So length of third side = 4 cm
39)दी गई आकृति में, यदि AB = 10 cm, \(\angle ABD = 90^0\) और AD = 17 cm तो CD की लंबाई कितनी है ?
SSC CGL 2020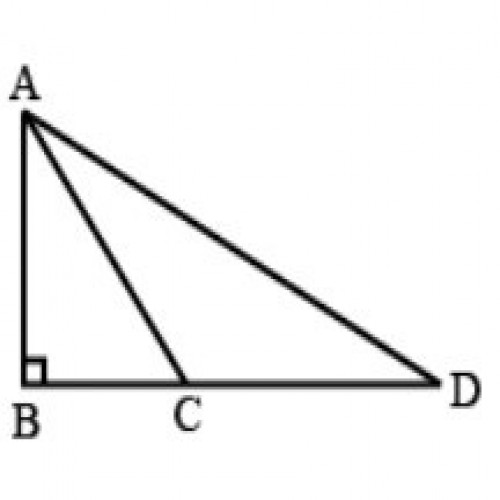
9 cm
In \(\triangle ABC\), AB = 8 cm ; AC = 10 cm; \(\therefore BC = \sqrt{AC^2-AB^2}=\sqrt{10^2-8^2}=6\space cm\); In \(\triangle ABD\), AD = 17 cm ; \(\therefore BD =\sqrt{AD^2-AB^2}=\sqrt{17^2-8^2}= 15 \space cm\) ; So CD = 15 - 6 = 9 cm
SSC CGL 202040)यदि एक समबाहु त्रिभुज़ का क्षेत्रफल \(36\sqrt3\space cm^2\) है, तो त्रिभुज़ का परिमाप बताइए ।
36 cm
Area of an equilateral triangle = \(36\sqrt3\space cm^2\); ⇒ \({\sqrt3\over4}\times Side^2= 36\sqrt3\); ⇒ Side = 12 cm ; Therefore, Perimeter of triangle = \(3\times Side\) = 36 cm
Full Syllabus in 1 Video [Contains Everything basic to advance]