objective Ques (11 results)
Class 10 Maths1)For what value of k, the pair of equations 4x – 3y = 9, 2x + ky = 11 has no solution?
-3/2
We have, 4x – 3y = 9 and 2x + ky = 11
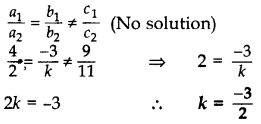
Class 10 Maths2)Solve the following pair of equations for x and y:
\({a^2 \over x} − {b2 \over y }= 0; {a^2b \over x}+{b^2a \over y} = a + b, x ≠ 0; y ≠ 0\)
\(x =a^2, y=b^2\)
Solution:
Class 10 Maths3)Solve for x and y:
27x + 31y = 85;
31x + 2 7y = 89
x = 2, y = 1
Solution:
Putting the value of ‘x’ in (i), we get
2 + y = 3 ⇒ y = 3 – 2 = 1
∴ x = 2, y = 1
Class 10 Maths4)The sum of the digits of a two digit number is 8 and the difference between the number and that formed by reversing the digits is 18. Find the number.
53
Solution:
Let unit and tens digit be x and y.
∴ Original number = 1x + 10y …(i)
Reversed number = 10x + 1y
According to question,
x + y = 8
⇒ y = 8 – x …(ii)
Also, 1x + 10y – (10x + y) = 18
⇒ x + 10y – 10x – y = 18
⇒ 9y – 9x = 18
⇒ y – x = 2 …[Dividing both sides by 9]
⇒ 8 – x – x = 2 …[From (ii)]
⇒ 8 – 2 = 2x
⇒ 2x = 6
From (ii), y = 8 – 3 = 5
From (i), Original number = 3 + 10(5) = 53
Class 10 Maths5)The age of the father is twice the sum of the ages of his 2 children. After 20 years, his age will be equal to the sum of the ages of his children. Find the age of the father.
40 yrs
Solution:
Let the present ages of his children be x years and y years.
Then the present age of the father = 2(x + y) …(i)
After 20 years, his children’s ages will be
(x + 20) and (y + 20) years
After 20 years, father’s age will be 2(x + y) + 20
According to the Question,
⇒ 2(x + y) + 20 = x + 20 + y + 20
⇒ 2x + 2y + 20 = x + y + 40
⇒ 2x + 2y – x – y = 40 – 20
⇒ x + y = 20 …[From (i)]
∴ Present age of father = 2(20) = 40 years
Class 10 Maths6)The pair of equations y = 0 and y = –7 has
No solution
The graph of equations will be parallel lines. So the equations have no solution.
Class 10 Maths7)The father’s age is six times his son’s age. Four years hence, the age of the father will be four times his son’s age. The present ages, in years, of the son and the father are, respectively
6 and 36
Let the age of father be x and of son is y.
Then according to question,
x = 6y …..(i)
Four years hence age of son will be y + 4 and age of father will be x + 4
Then according to question,
x + 4 = 4 (y + 4)
x – 4y = 12 …..(ii)
Solving equations (i) and (ii) we get:
y = 6 and x = 36
Class 10 Maths8)A man earns ₹600 per month more than his wife. One-tenth of the man’s salary and l/6th of the wife’s salary amount to ₹1,500, which is saved every month. Find their incomes
Wife’s income = ₹5,400
Man’s income = ₹6,000
Class 10 Maths9)Graphically, the pair of equations 7x – y = 5; 21x – 3y = 10 represents two lines which are
parallel
Class 10 Maths10)The pair of equations 3x – 5y = 7 and – 6x + 10y = 7 have
no solution