objective Ques (100 results)
SSC CGL 20201)The length, breadth and height of a cuboidal box are in the ratio 7 : 5 : 3 and its whole surface area is 27832 sq cm. Its volume is :
288120 \(cm^3\)
l = 7 k cm, b = 5 k cm. h = 3 k cm. TSA = 27832sq.cm. ⇒2 (lb + bh + hl) = 27832 ⇒ k = 14
l = 98cm, b= 70cm, h = 42cm
volume of cuboidal box =( 98 x 70 x 42) cu. cm = 288120 cu cm
SSC CGL 20192)A right circular cylinder of maximum volume is cut out from a solid wooden cube.The material left is what percent of the volume (nearest to an integer) of the original cube?
21
Side of cube = a;
Volume of cube =\( a^3;\)
For the maximum volume,
Height of right circular cylinder = a;
Diameter = a;
Radius =\( a/2;\)
Volume of right circular cylinder = \(\pi r^2 h = \frac{22}{7} \times (\frac{a}{2})^2 \times a = \frac{11}{14}a^3 =0.78a^3;\)
Material left = \(a^3 - 0.7857a^3 = 0.2143a^3;\)
Percentage material left = \(\frac{0.2143a^3}{a^3} \times 100 = 21.43 \approx 21%\)
SSC CGL 20193)If the radius of the base of a cone is doubled, and the volume of the new cone is three times the volume of the original cone, then what will be the ratio of the height of the original cone to that of the new cone?
4 : 3
Volume of the cone =\( \frac{1}{3} \times \pi r^2 h;\)
\(\frac{v_1}{v_2} = \frac{(r_1)^2(h_1)}{(r_2)^2(h_2)};\)
\(\frac{h_1}{h_2} = \frac{(r_1)^2(v_2)}{(r_2)^2(v_1)};\)
\(\frac{h_1}{h_2} = \frac{(2r_1)^2(v_2)}{(r_2)^2(3v_2)};\)
\(h_1 : h_2 = 4 : 3\)
SSC CGL 20194)If the diameter of the base of a cone is 42 cm and its curved surface area is 2310 \({cm}^2\), then what will be its volume (in \({cm}^3\))?
12936
Diameter of the base of a cone = 42 cm;
radius(r) = 42/2 = 21 cm;
Curved surface area =\( 2310 cm^2;\)
\(\pi r l \)= 2310;
\(\frac{22}{7}\times 21 \times l \)= 2310;
l = 35;
\(l^2 = r^2 + h^2;\)
\(35^2 = 21^2 + h^2;\)
\(h^2 = 1225 - 441 = 784;\)
h = 28 cm;
Volume = \(\frac{1}{3} \pi r^2 h = \frac{1}{3} \times \frac{22}{7} 21^2 \times 28
= 12936 cm^3\)
SSC CGL 20195)If a cuboid of dimensions 32 cm x 12 cm x 9 cm is cut into two cubes of same size, what will be the ratio of the surface area of the cuboid to the total surface area of the two cubes?
65 : 72
For big cuboid,
l = 32 cm, b = 12 cm, h = 9 cm;
Surface area = \(2(l \times b + b \times h + h \times l)\)
= \(2(32 \times 12 +12 \times 9 + 9 \times 32)\) = 2(384 + 108 + 288) = 1560
Assume that cuboid is melted to same size of cube so,
\(l \times b \times h = 2 \times a^3;\)
\(32 \times 12 \times 9 = 2 \times a^3;\)
\(1728 = a^3;\)
a = 12 cm;
Surface area of cube =\( 6 \times 12^2 \)= 864;
Ratio of the surface area of the cuboid to the total surface area of the two cubes = \(1560 : 2 \times 864 \)= 65 : 72
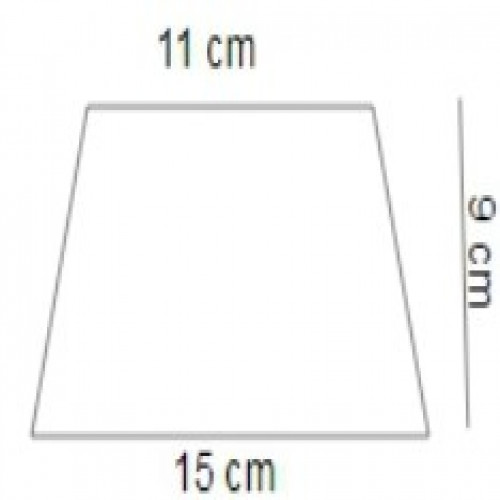
SSC CGL 20196)The base of right prism is a trapezium whose parallel sides are 11 cm and 15 cm and the distance between them is 9 cm. If the volume of the prism is 1731.6\( cm^3,\) then the height(in cm) of the prism will be:
14.8
Volume = area of base \times height ;
Base area =\( \frac{1}{2} \times (l_1 + l_2) \times\) h =\( \frac{1}{2} \times (11 +15) \times 9\) = 117 \(cm^2\)
Height =\( \frac{volume}{base area}\) = \(\frac{1731.6}{117}\) = 14.8 cm
SSC CGL 20197)The lateral surface area of a cylinder is \(352 cm^2\). If its height is 7 cm, then its volume(in \(cm^3\)) is: (Take\( \pi = \frac{22}{7}\))
1408
The lateral surface area of a cylinder =\( 352 cm^2.\)
\(2\pi r h \)= 352
\(2\pi r \times 7\)= 352
r = \(\frac{176}{7\times 22/7} \)= 8
Volume = \(\pi r^2 \times h\) = \(\frac{22}{7} \times(8)^2 \times 7\)
= \(1408 cm^3\)
SSC CGL 20198)The internal and external radii of a hollow hemispherical vessel are 6 cm and 7 cm respectively. What is the total surface area (in \(cm^2\)) of the vessel?
\(183 \pi\)
Total surface area of the vessel = External surface area + internal surface area + upper portion area
r1 = 6 cm;
r2 = 7 cm;
= \(2 \pi (r2)^2 + 2 \pi (r1)^2 + \pi ((r2)^2 - (r1)^2)
= \pi[2 \times 7^2 + 2 \times 6^2 + (r2)^2 - (r1)^2]
= \pi[98 + 72 + 49 - 36] = 183\pi\)
SSC CGL 20199)Three solid metallic spheres whose radii are 1 cm, X cm and 8 cm, are melted and recast into a single solid sphere of diameter 18 cm. The surface area (in \(cm^2\)) of the sphere with radius x cm is:
\(144 \pi\)
Volume of solid sphere =\( \frac{4}{3} \pi r^3\);
Radius of single solid sphere = 18//2 = 9 cm;
Volume of single solid sphere = Volume of three solid metallic spheres;
\(\frac{4}{3} \pi (9)^3 = \frac{4}{3} \pi[1^3 + x^3 + 8^3];\)
729 = 512 + 1 + \(x^3\);
\(x^3\)= 216;
x = 6 cm;
Surface area = \(4\pi r^2 = 4\pi 6^2 = 144 \pi\)
SSC CGL 201910)If the radius of a sphere is increased by 4 cm, its surface area is increased by \(464 \pi cm^2\) . What is the volume(in \(cm^3\)) of the original sphere?
\(\frac{15625}{6}\pi\)
Difference in the surface area =\( 464 \pi;\)
\(4\pi(r + 4)^2 - 4\pi r^2 = 464 \pi;\)
\(4\pi[r^2 + 16 + 8r - r^2] = 464 \pi;\)
16 + 8r = 116;
r = 100/8 = 25/2 cm;
Volume of the the sphere =\( \frac{4}{3} \pi r^3 = \frac{4}{3} \pi (25/2)^3 = \frac{15625}{6} \pi\)