Definitions

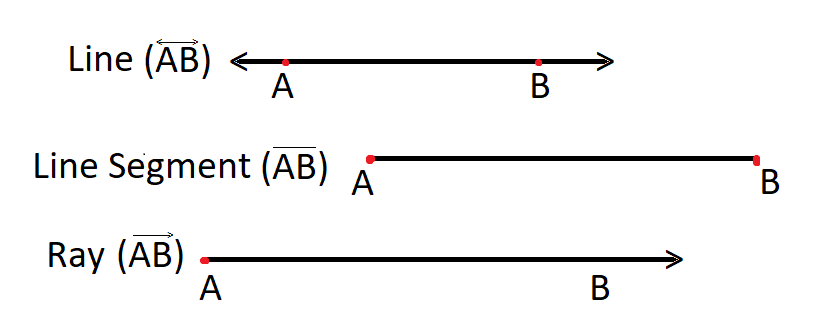
Line:- A set of infinite points with length but no width. A line has no endpoint.

Line segment:-  A line segment is similar to a line with two endpoints

Ray:- A ray is also similar to a line with one endpoint.

Types of Lines

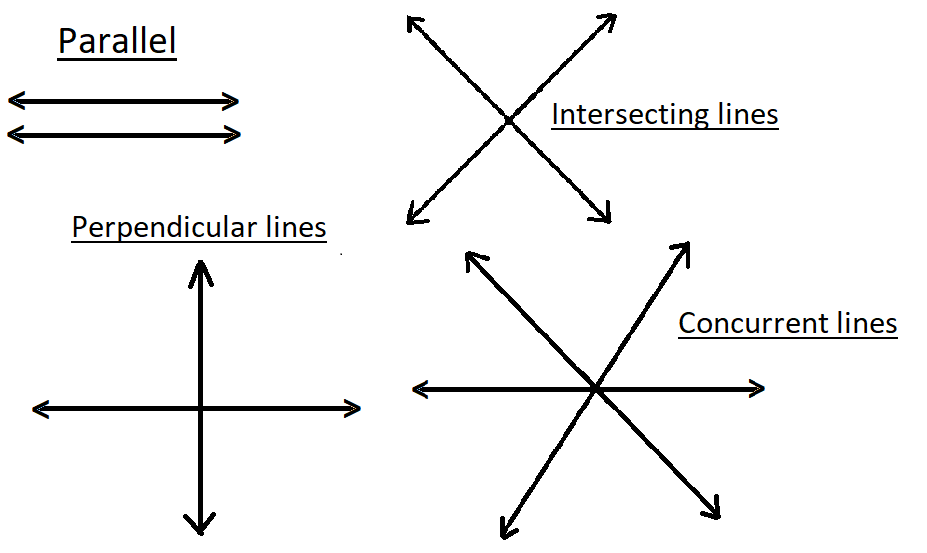
Parallel lines:- If two lines have no point in common they are said to be parallel to each other.

Intersecting lines:- If two lines intersect at a point they are said to be intersecting lines.

Perpendicular lines:- If two lines one vertical and the other horizontal intersect at a point they are said to be perpendicular lines.

Concurrent lines:- If more than two lines intersect at a common point they are said to be concurrent lines.

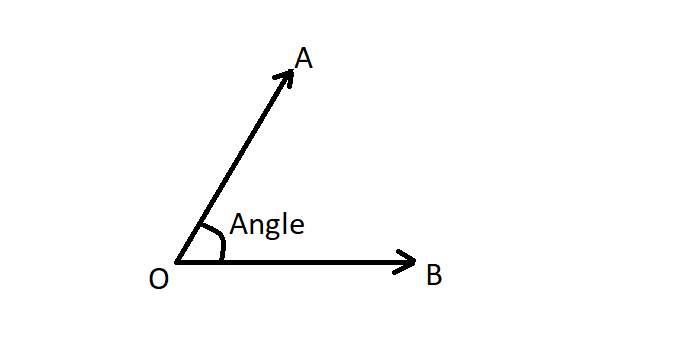
Angle:- Angle is defined as a figure formed when two rays meet at a point. It is represented by the symbol ∠. In the figure, the angle is ∠AOB. Point O is the vertex.

Degree ⇔ Radian Conversion

Angle is usually denoted by degree (°) like 0°, 45°, 90° 180° etc. It can also be represented by radian. To convert radian to degree or vice-versa it is recommended to learn the value of pi (π) in radian and degree. The value of π is 3.14 (22/7) in radian and 180° in degree.

Thus 3.14 radian = 180° [use unitary method for conversion] (1 radian = 180°/ 3.14  OR 1° = 3.14/180 )

Types of Angle

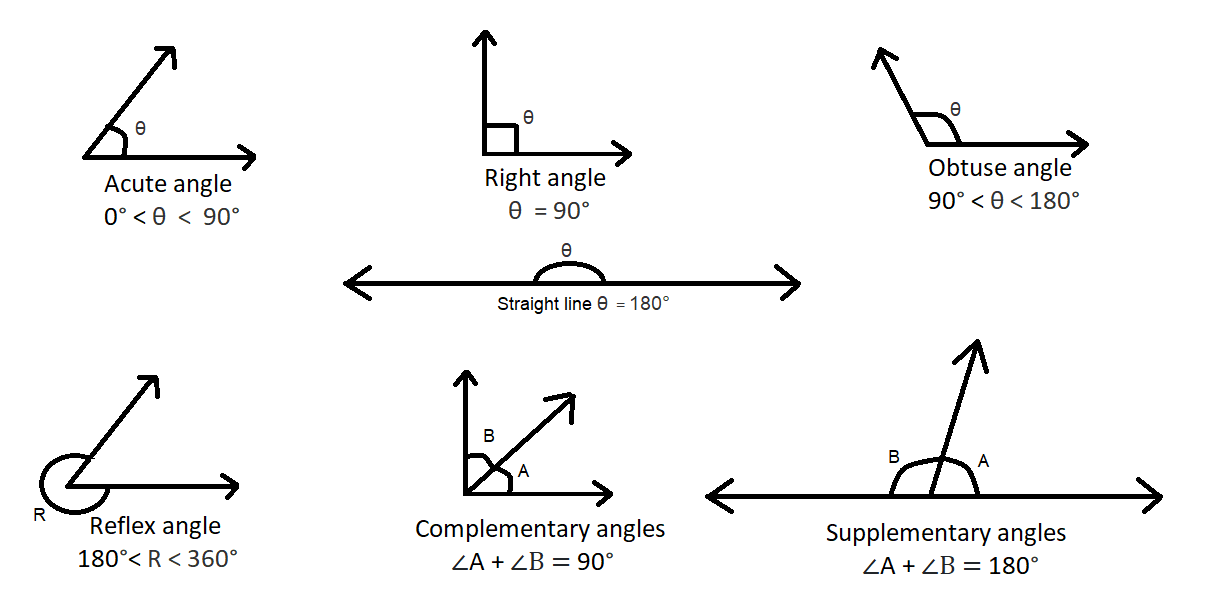
1) Acute Angle: Angles whose value is less than 90° are called Acute Angle.

2) Right Angle: Angles whose value is equal to 90° are called Right Angle. 

3) Obtuse Angle: Angles whose value is greater than 90° but less than 180° are called Obtuse Angle. 

4) Straight line: When the value of angle is 180° it becomes a straight line.

5) Reflex Angle: Angles whose value is greater than 180° but less than 360° are called Reflex Angle. 

6) Complementary Angles: When the sum of the measures of the two angles is 90°, the angles are called Complementary Angle. ∠A + ∠B = 90°

7) Supplementary Angles: When the sum of the measures of the two angles is 180°, the angles are called Supplementary Angle.∠A + ∠B = 180°